Prawo załamania, prawo odbicia - skąd się biorą?

I skąd psy wiedzą jak ich używać?

Wszyscy znamy ze szkoły prawo załamania i odbicia światła. Używanie ich nie stanowi zwykle większego problemu. Często jednak wymaga przeprowadzenia szybkich szybkich obliczeń (takich jak obliczanie sinusa kąta), które raczej ciężko przeprowadzić w głowie. Ciężko dla nas, ale jak się okazuje – nie dla psów!

Tim Pennings matematyk z Davenport University bawił się ze swoim corgi – Elvisem nad jeziorem. Tim rzucał piłkę a zadaniem Elvisa było jak najszybciej ją złapać. Realizował zadanie, jak można by się spodziewać – biegnąc wzdłuż linii prostej łączącej jego położenie z miejscem, w którym wylądowała piłka. Nic nadzwyczajnego, jednak w pewnym momencie Tim rzucił piłkę w taki sposób, że wylądowała w wodzie. Elvis momentalnie obrał nową strategię złapania piłki. Nie biegł już po linii prostej, tylko po prostej łamanej. Zupełnie tak, jakby tor jego ruchu się załamywał na brzegu jeziora. Tim policzył szybko i sprawdził, że jego pies idealnie wyznaczył kąt, pod jakim jego trajektoria powinna się załamać przy przejściu przez powierzchnię wody, aby czas dogonienia piłki był jak najkrótszy. Jak to możliwe, że pies tak szybko to policzył!?

Do Dogs Know Calculus? – Timothy J. Pennings

I przede wszystkim jak w ogóle obliczyć taki kąt?

Skoro pies umie liczyć takie rzeczy w jego psim móżdżku, to my też się nauczymy! Zacznijmy od zdefiniowania praw załamania i odbicia, potem ustalimy skąd te prawa się biorą. Ostatecznie doprowadzi nas to do odpowiedzi na pytanie: jak powtórzyć wyczyn Elvisa?

Prawo załamania i odbicia

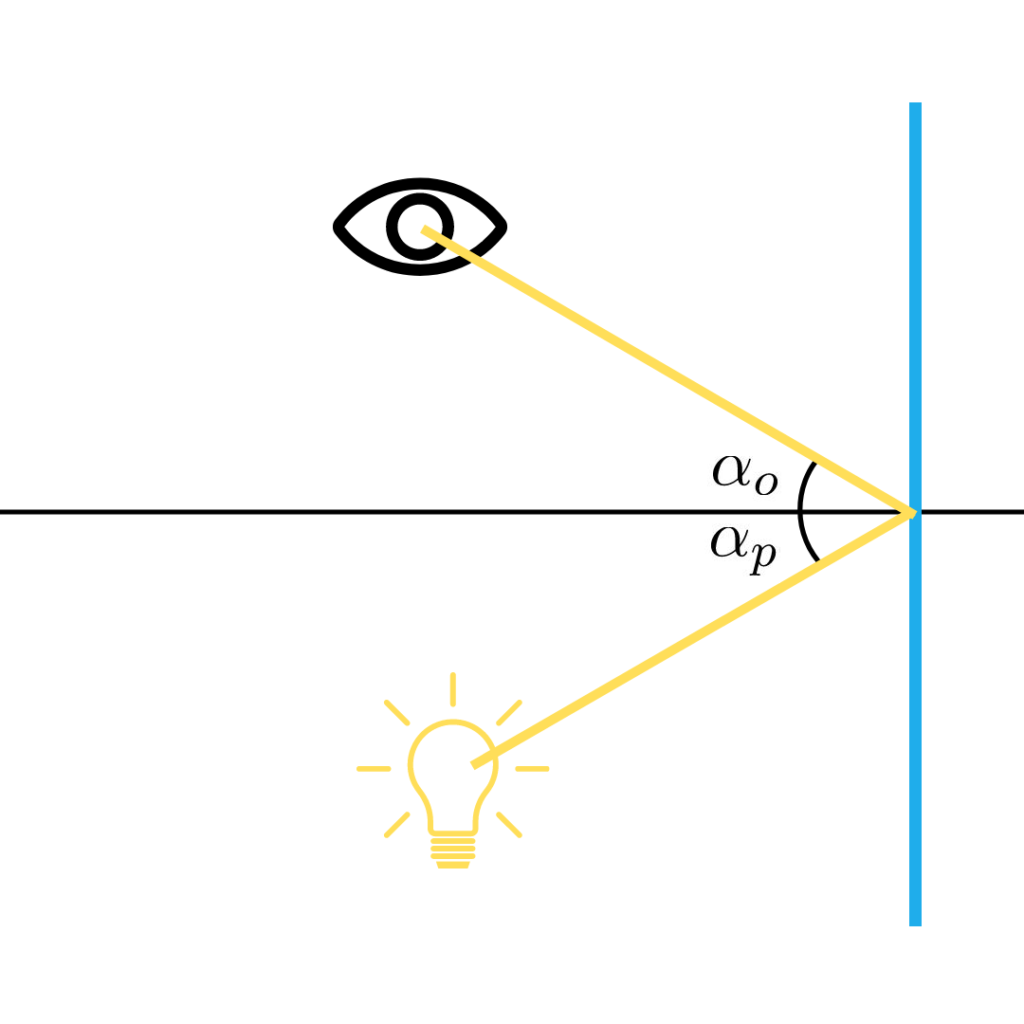
Najpierw prawo odbicia – mówi nam, że kąt odbicia światła od powierzchni jest równy kątowi padania.

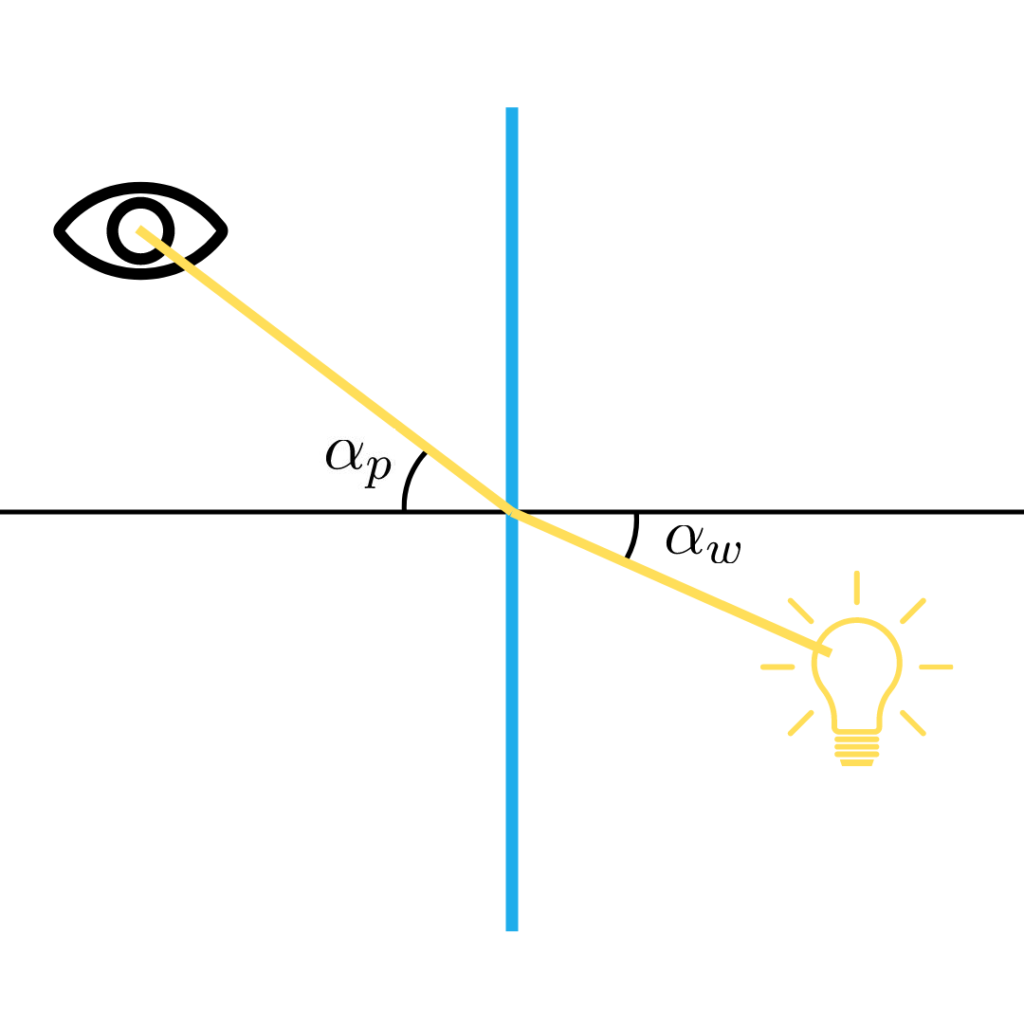
Prawo załamania, zwane również prawem Snella, wiąże kąt padania oraz kąt załamania światła przy przejściu przez granicę ośrodków. Robi to w następujący sposób:

$\alpha_p=\alpha_o$ .
$n_p=\frac{c}{v_p}$
$n_w=\frac{c}{v_w}$
$n_p sin \alpha_p=n_w sin \alpha_w$

Gdzie n_p i n_w to współczynnik załamania odpowiednio w pierwszym ośrodku (np. powietrzu) i w drugim ośrodku (np. w wodzie). v_p i v_w to prędkości światła w ośrodkach, a c to prędkość światła w próżni.

Możesz zwizualizować sobie prawa załamania i odbicia bawiąc się tą symulacją.

Skąd biorą się opisane wcześniej prawa?

W szkole uczymy się prawa Snella i prawa odbicia, jak regułek danych odgórnie. Pytanie: „skąd te prawa się wzięły?” – wydaje się być wręcz nielegalne. Na pytania bardziej ciekawskich uczniów nauczyciele odpowiadają, że są to prawa odkryte doświadczalnie. I rzeczywiście początkowo tak było. Teraz jednak świetnie znamy źródło praw Snella i odbicia.

Źródłem tych praw jest zasada Fermata, czyli optyczna wersja zasady najmniejszego działania.

Co ta zasada mówi?

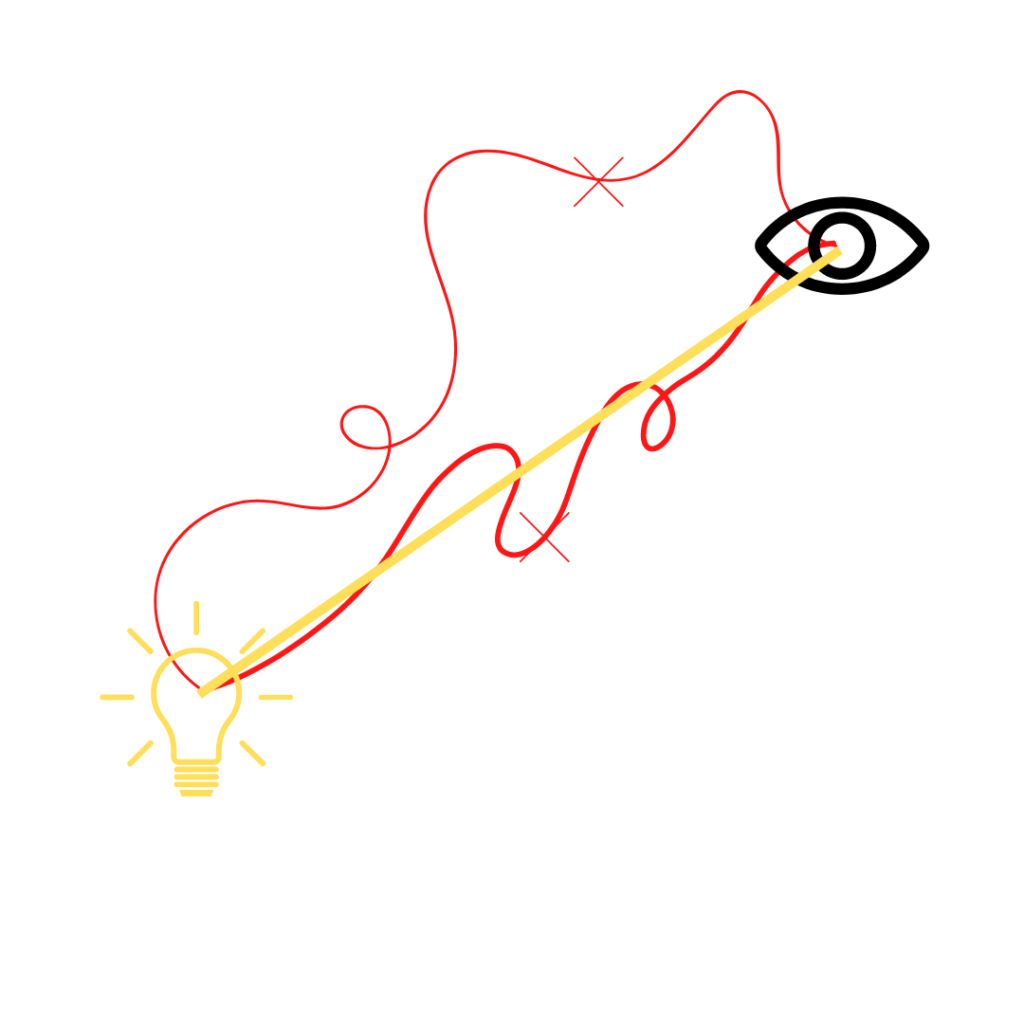
Mówi ona, że światło biegnące między dwoma punktami A i B wybierze taką drogę, której pokonanie zajmie najmniej czasu. W przypadku gdy oba punkty A i B znajdują się w jednym ośrodku (np. w powietrzu) wniosek jest bardzo prosty – światło będzie poruszało się po linii prostej.

Ale co, gdy skomplikujemy sytuację i dodamy granicę ośrodków do naszego rysunku?

Prawo Odbicia – Wyprowadzenie

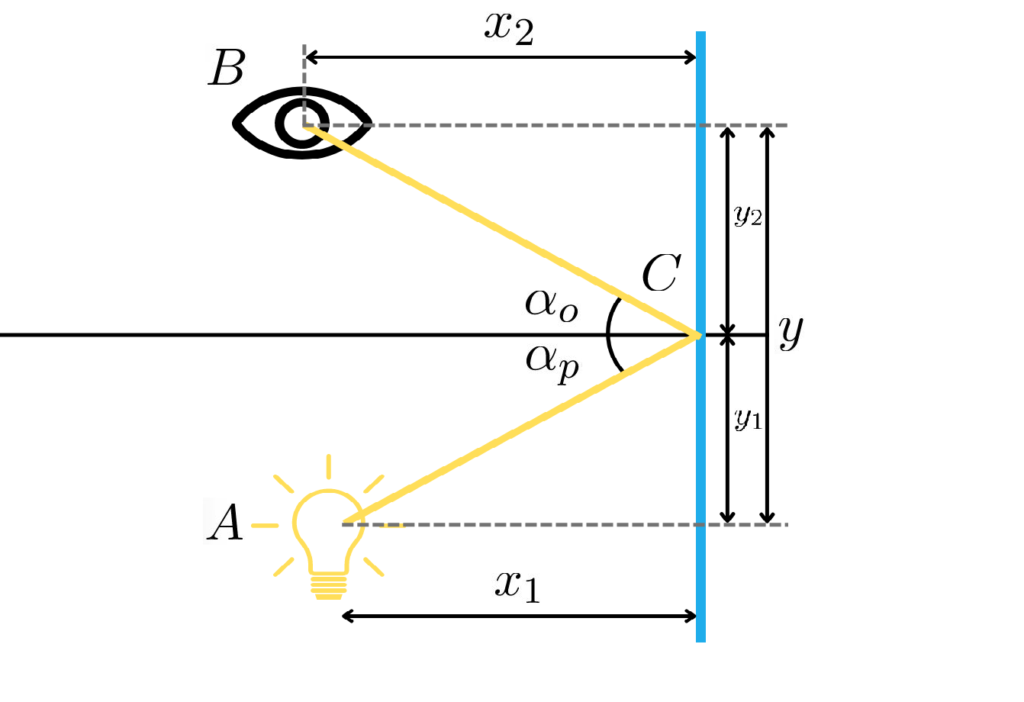
Jaką drogę wybierze światło, zgodnie z zasadą Fermata, aby przedostać się z punktu A do B odbijając się przy tym od lustra?

Powiedzmy, że światło odbije się od lustra w punkcie C. Wiemy że drogi A-C i B-C będą liniami prostymi ponieważ dowolna inna realizacja wydłuży czas przebycia przez światło drogi A-B. Zatem jedyne pytanie jakie nam pozostaje to: w jakim miejscu znajdzie się punkt C?

Aby to wyznaczyć wprowadźmy następujące oznaczenia:

$t=t_{AC}+t_{BC}$

$S_{AC}=\sqrt{x^{2}_{1}+y^{2}_{1}}$
$t_{AC}=\frac{S_{AC}}{v}$
$S_{CB}=\sqrt{x^{2}_{2}+(y-y_1)^2}$
$t_{CB}=\frac{S_{CB}}{v}$

Aby znaleźć $y_1$ , które minimalizuje czas – liczymy pochodną:
$\frac{dt}{dy_1}=\frac{y_1}{v\sqrt{x^{2}_{1}+y^{2}_{1}}}-\frac{y-y_1}{v\sqrt{x^{2}_{1}+(y-y_1)^2}}}$
$\frac{dt}{dy_1}=v sin\alpha_p - v sin\alpha_o$

Dla minimalnej trajektorii mamy:
$\frac{dt}{dy_1}=v sin\alpha_p - v sin\alpha_o = 0$
$sin\alpha_p =sin\alpha_o$
$\alpha_p =\alpha_o$

Udowadniamy zatem ostatecznie, że kąt padania musi równać się kątowi załamania!

Prawo Snella – Wyprowadzenie

Postąpimy tutaj podobnie, jak w poprzednim rozdziale i zaczniemy od pytania:

Jaką drogę zgodnie z zasadą Fermata wybierze światło, aby przemieścić się między punktami A i B, które znajdują się po różnych stronach granicy ośrodków?

W różnych ośrodkach światło porusza się z różną prędkością określoną przez współczynnik załamania światła. Podobnie jak poprzednio – nazwiemy punkt przekroczenia granicy jako C. Światło na drogach A-C i B-C będzie poruszało się po liniach prostych. Dla nas pozostaje jedynie do ustalenia gdzie znajduje się punkt C.

$n_p=\frac{c}{v_p}$
$n_w=\frac{c}{v_w}$

$t=t_{AC}+t_{BC}$

$S_{AC}=\sqrt{x^{2}_{1}+y^{2}_{1}}$
$t_{AC}=\frac{S_{AC}}{v_w}$
$S_{CB}=\sqrt{x^{2}_{2}+(y-y_1)^2}$
$t_{CB}=\frac{S_{CB}}{v_p}$

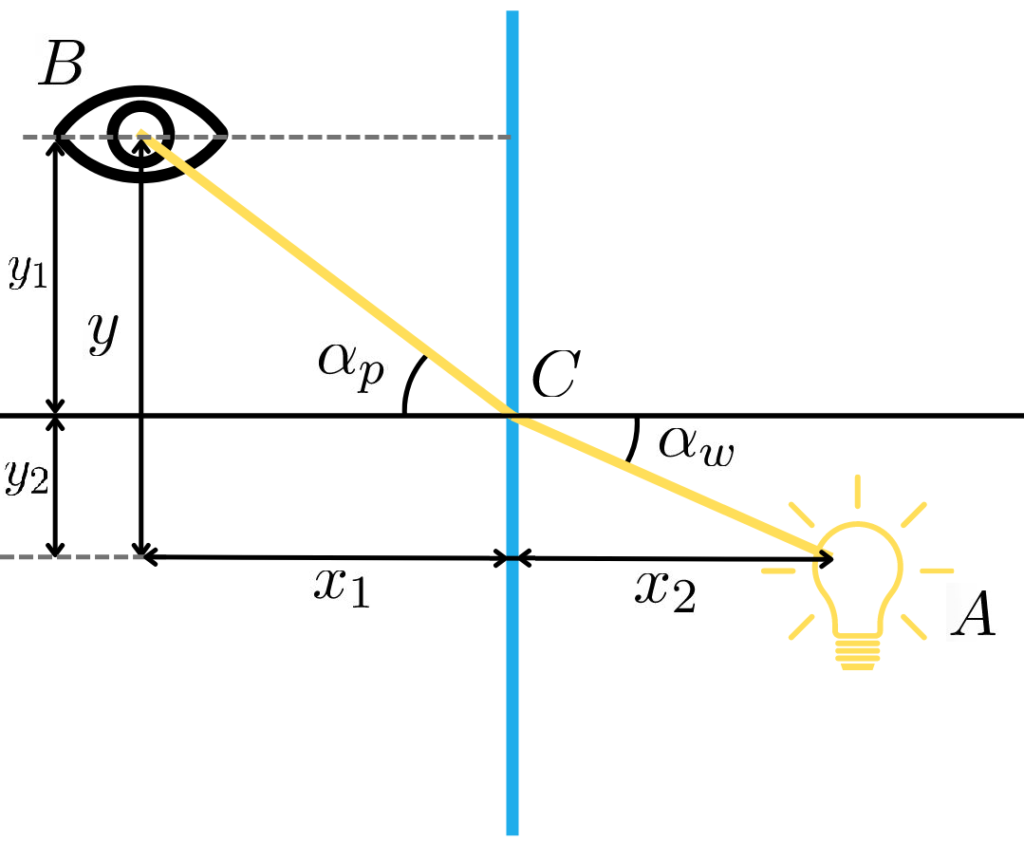
Aby znaleźć $y_1$ , które minimalizuje czas – liczymy pochodną:

$\frac{dt}{dy_1}=\frac{y_1}{v_p\sqrt{x^{2}_{1}+y^{2}_{1}}}-\frac{y-y_1}{v_w\sqrt{x^{2}_{1}+(y-y_1)^2}}}$
$\frac{dt}{dy_1}=\frac{sin\alpha_p}{v_p} -\frac{sin\alpha_o}{v_w}$

Dla minimalnej trajektorii mamy:

$\frac{dt}{dy_1}=\frac{sin\alpha_p}{v_p} -\frac{sin\alpha_o}{v_w}=0$
$\frac{sin\alpha_p}{v_p} =\frac{sin\alpha_o}{v_w}$

$n_psin\alpha_p =n_wsin\alpha_w$

Ostatecznie otrzymujemy dobrze znane prawo Snella.

Zasada najmniejszego działania

Widzimy, że zasada Fermata zawiera w sobie prawo odbicia i prawo Snella i jednoznacznie definiuje zachowanie światła.

Ale skąd bierze się zasada Fermata?

Trochę to wygląda tak jakbyśmy zastąpili kilka intuicyjnych praw jendym znacznie mniej intuicyjnym. Czy taka zamiana to dobry deal? Zdecydowanie tak!

Zasada najmniejszego działania działa nie tylko w optyce, ale również w mechanice oraz chemii. Dyktuje ruch cząstek, zachowanie planet, silników, czy reakcji chemicznych. Jest więc bardzo fundamentalna i ze względu na to, cała nowoczesna mechanika klasyczna jest sformułowana w języku wychodzącym z zasady najmniejszego działania.

A skąd się bierze zasada najmniejszego działania?

Przez długi czas zasada najmniejszego działania była uznawana za ciekawostkę matematyczną. Fakt, że istnieje pewna niemierzalna doświadczalnie funkcja fizyczna nazywana działaniem, która na realnie realizowanej trajektorii przyjmuje wartość minimalną wydaje się bardzo dziwny i ciężki do ugryzienia przez fizyka. Btw. działanie dla światła to czas pokonania trajektorii.

Od dobrych kilkudziesięciu lat wiemy, co stoi za zasadą najmniejszego działania.

Jest to mechanika kwantowa, ale taka dziwna, sformułowana w języku całek po trajektorii. Jest to zupełnie bezużyteczne sformułowanie do obliczeń, ale wprost wspaniałe do wyciągania ogólnych wniosków o świecie. Richard Feynman zauważył, że działanie naturalnie pojawia się w tym sformułowaniu. Sprawia, że cząstka (np. foton) z bardzo małym prawdopodobieństwem wybierze trajektorię odpowiadającą małemu działaniu, a z dużym prawdopodobieństwem, dużemu działaniu. Mówiąc po “klasycznemu” a nie “kwantowemu” – cząstka wybierze trajektorię odpowiadającą najmniejszemu działaniu.

Wydaje mi się to niesamowite, że proste prawa rządzące naszym światem takie jak prawo załamania, odbicia, czy fakt, że podrzucona piłka będzie poruszała się po paraboli – mają swoje źródło w mechanice kwantowej.

Ale wróćmy z tych głębokich rozważań nad naturą rzeczywistości do Elvisa.

Jak pies używa zasady najmniejszego działania?

Przypomnijmy, że podczas aportowania najważniejsze w życiu Elvisa jest jak najszybsze złapanie piłki. W związku z tym, w optymalnej sytuacji powinien zachowywać się dokładnie tak samo jak foton i w taki sam sposób wybrać trajektorię, po której będzie gonił piłkę. I rzeczywiście, okazuje się, że pies stosuje się do prawa Snella i zmienia ośrodki wchodząc do wody w takim punkcie, dla którego spełnione jest:

$\frac{sin\alpha_p}{v_p}=\frac{sin\alpha_w}{v_w}$
$v_w$ – prędkość Elvisa w wodzie
$v_p$ – prędkość Elvisa na piasku

Jak to możliwe, że pies umie wyznaczyć optymalną trajektorię w swojej uroczej głowie, a wielu studentów fizyki nie?! To pytanie prawdopodobnie należy skierować do naukowców zajmujących się ewolucją instynktownych zachowań u ssaków.

Jednak sam fakt, że pies instynktownie jest w stanie wyznaczyć drogę w myśl zasady najmniejszego działania, do której pełnego zrozumienia ludzkość potrzebowała głębokiego wglądu w mechanikę kwantową, wydaje się oszałamiający!

No cóż, teraz nie tylko Elvis, ale również Ty wiesz jak wyznaczyć optymalny kąt wejścia do wody. Pytanie, czy umiesz zastosować zasadę Fermata na polu bitwy – rozwiązując zadanie olimpijskie?

Zadanie – zasada Fermata

Promień światła emitowany jest z jednorodnego źródła światła umieszczonego w punkcie: $\frac{1}{\epsilon^2}$

Przestrzeń wypełniona jest tajemniczym ośrodkiem, której współczynnik załamania zmienia się wraz z odległością od osi y – n(x). Wyznacz drogę po jakiej będą się poruszały promienie wylatujące ze źródła i znajdź kąt emisji dla którego promień światła dotrze do punktu (3,2).

$n(x)=\epsilon\sqrt{x}$

Rozwiązanie zadania za pomocą zasady Fermata

$sin\alpha_0=n(\Delta x)sin\alpha_1$
$n(\Delta x)sin\alpha_1=n(2\Delta x)sin\alpha_2$

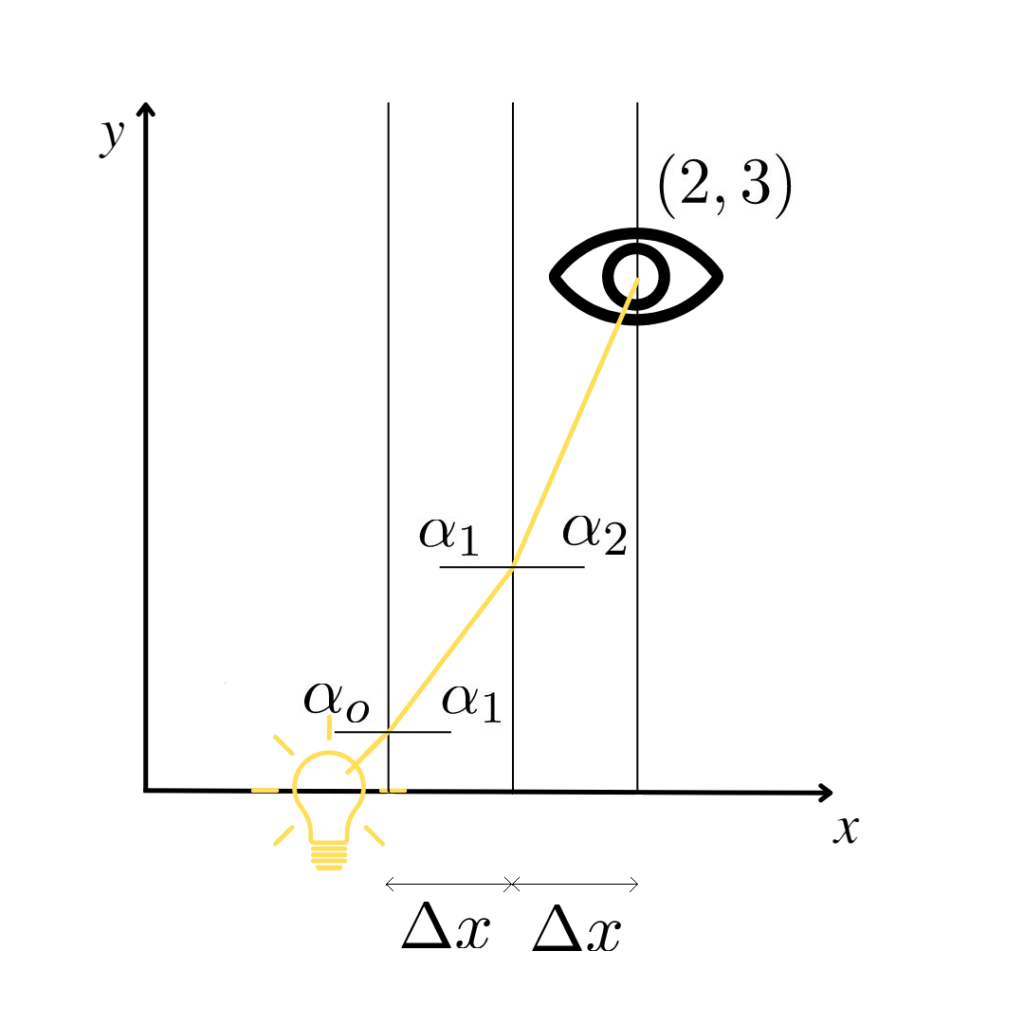
Widać, że współczynnik załamania światła kąta razy sinus kąta między promieniem a osią y jest niezmiennikiem.

Możemy zatem zapisać:
$sin\alpha_0=n(x)sin\alpha(x)$

Korzystając z następujących relacji:

$sin\alpha(x)=\frac{tan\alpha}{\sqrt{1+tan^2\alpha}}$
$tan \alpha=\frac{dx}{dy}=\frac{1}{y'}$

gdzie $y(x)$ to funkcja określająca trajektorię promienia.

Możemy wyznaczyć tę trajektorię następująco:
$n(x)=\epsilon\sqrt{x}$
$\epsilon=\frac {1}{\sqrt{m}}$
$\sin\alpha_o=n(x) \frac {1}{\sqrt{1+y'^2(x)}}$

gdzie $y(x)$ to funkcja określająca trajektorię promienia.

Możemy wyznaczyć trajektorię następująco:

$y'=\frac{n(x)^2}{sin^2\alpha}-1=\frac{\epsilon^2x}{sin^2\alpha}$
$y=\int\frac{\epsilon^2x}{sin^2\alpha}dx$
$y(x)=\frac{\epsilon^2x^2}{2sin^2\alpha}+C$

Z położenia punktu startowego promienia wyznaczamy C

$y(x)=\frac{\epsilon^2x^2-1}{2 sin^2\alpha}$

Stąd wyznaczamy kąt $\alpha$ i podstawiamy współrzędne końcowego położenia promienia:

$sin\alpha =\sqrt{\frac{\epsilon^2 x^2-1}{2y(x)}}$
$sin\alpha=\frac{1}{\sqrt{2}}$
$\alpha=45^{\circ}$

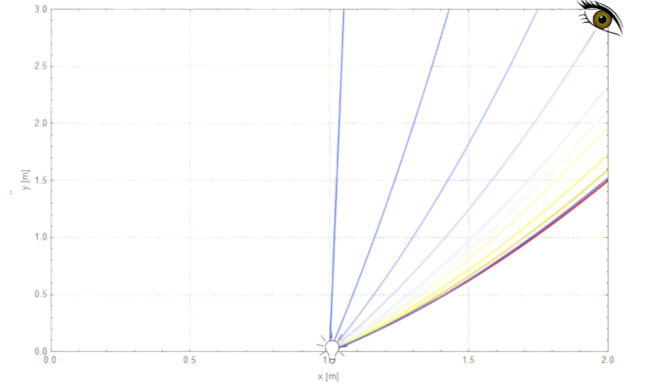
sposób poruszania się światła w ośrodku- wykres

Jak widzimy, w naszym dziwnym ośrodku światło porusza się po linii prostej tylko dla kąta 0° – czyli poruszając się pionowo w górę. Ponadto istnieje obszar „zakazany” dla światła, którego nigdy nie będziemy w stanie oświetlić.

To zadanie przypomina zadanie z Olimpiady Fizycznej OF 1974/1975 z III etapu oraz zadanie z Międzynarodowej Olimpiady Fizycznej IPHO 2015.

Prawo załamania – podsumowanie

Mam nadzieję, że ten artykuł pomógł Ci dowiedzieć się czym jest prawo odbicia i prawo załamania oraz pokazał Tobie, jak prawidłowo korzystać z zasady Fermata. Artykuł został napisany przez naszych tutorów, którzy na co dzień prowadzą zajęcia najambitniejszym uczniom w Polsce. Jeżeli chciałbyś dowiedzieć się więcej o tych, bądź o innych zjawiskach fizycznych – zapisz się na nasze korepetycje! Jako doświadczeni korepetytorzy, potrafimy wyjaśnić każde niezrozumiałe przez Ciebie zjawisko fizyczne. Z nami fizyka w cale nie jest aż taka trudna!

Korepetycje Olimpijskie

Dla szkoły podstawowej

Dla licealistów

Dla studentów

Matura Międzynarodowa

Nasz zespół

Misja

Prawo załamania, prawo odbicia – skąd się biorą?